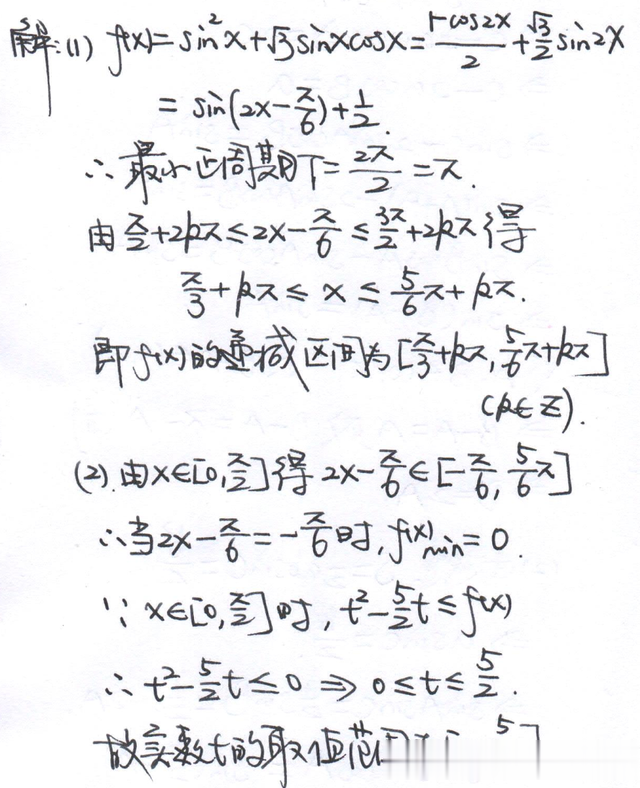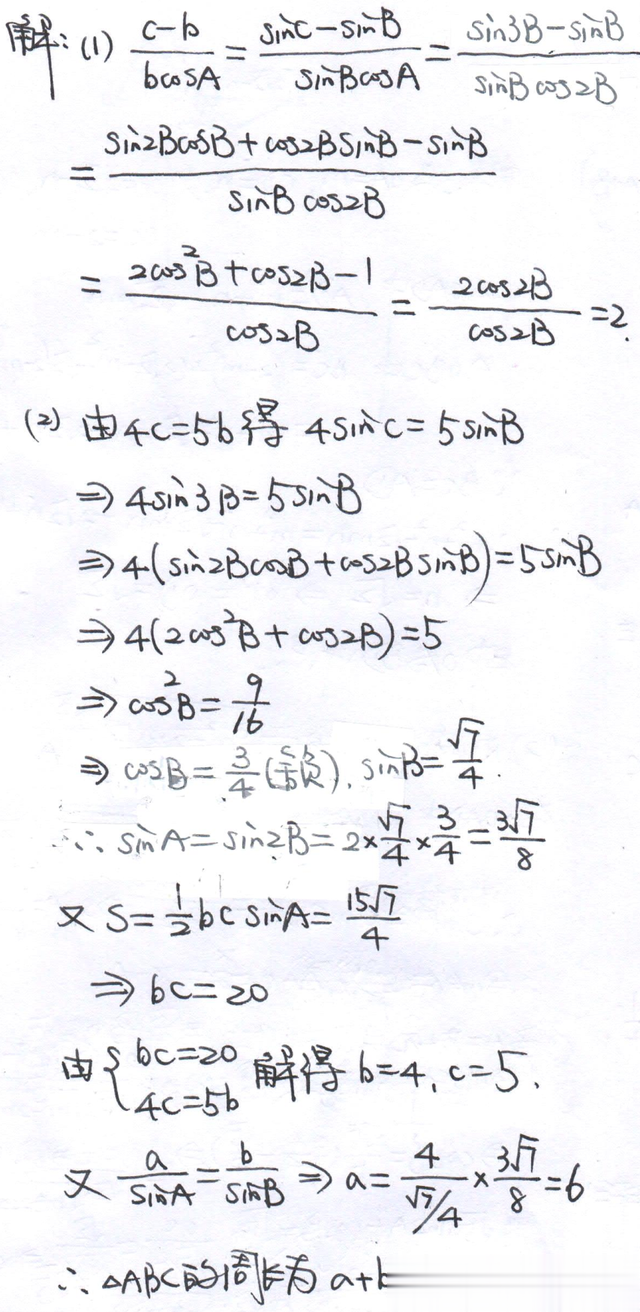核心考点预测
三角函数的图像与性质
重点题型:函数的周期性、单调性、对称性、极值问题。
创新方向:结合零点问题考查周期性,如“已知函数在区间内有3个零点,求参数范围”;通过图像变换(平移、伸缩)综合考查参数的求解;与导数结合,研究三角函数的切线、极值等综合问题。
三角恒等变换与化简求值
高频考点:利用诱导公式、和差角公式、二倍角公式进行化简;辅助角公式的应用;
易错点:符号判断错误(如诱导公式中象限对符号的影响)、角度的拆分与组合。
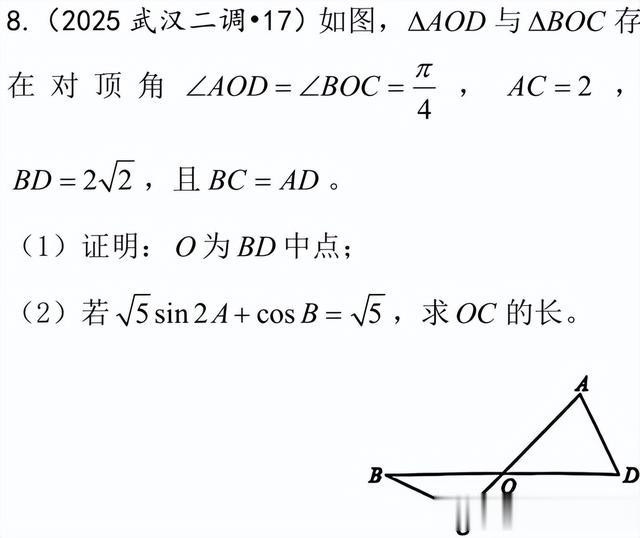
解三角形的综合应用
命题热点:正余弦定理与三角形面积公式的结合,求周长、面积或角度的最值;三角形中的中线、角平分线、高线问题,如“已知中线长求边长”;实际应用题(如测量问题、物理中的矢量分析),需结合仰角、俯角等几何模型。
难点:边角互化时的多解性分析(如正弦定理中“已知两边及一对角”的情况)。
与其他知识的交汇考查
与向量结合:利用向量垂直或共线条件求解三角形参数;
与数列结合:周期性变化模型(如人口增长、资源消耗)的三角函数表达;
与导数结合:研究三角函数的最值或单调性。
创新题型与情境预测
结构不良问题:提供多个条件(如边、角、面积),由考生选择部分条件求解三角形,体现思维灵活性。
实际情境建模:周期性现象(如气温变化、潮汐规律)的三角函数建模,需结合参数的实际意义分析。
开放探究题:如“已知三角形某边上的中线长,探究三角形形状或参数关系”。
备考策略与易错提醒
基础强化:
公式系统化:梳理同角关系、诱导公式、和差公式的内在联系,强化变形技巧(如切化弦、角度的拆分);
图像特征记忆:掌握三角函数的标准图像及其变换规律,快速判断参数对图像的影响。
解题技巧:
整体代换思想:将复杂角视为整体,简化单调性、对称性分析;
边角互化选择:优先使用正弦定理进行角化边,避免余弦定理的复杂计算。
易错点规避:
符号错误:诱导公式中根据象限判断符号,避免因忽略象限导致错误;
多解遗漏:使用正弦定理时,注意 可能对应锐角或钝角两种情况;
单位统一:实际问题中角度与弧度的转换需一致。